Quantitative Analysis is pursued with the objective of assessing performance properties for a HQPN. Different performance measures are offered for
QPN-Tool offers in its current version two main options for a quantitative analysis: conventional and structured. The conventional analysis technique transforms the HQPN into a flat QPN model, maps this QPN model onto a corresponding Markov chain, and subsequently analyses this chain with respect to its steady state distribution. The QPN's state space is fully explored causing quantitative analysis to be restricted to QPNs with a finite state space of acceptable size.
The conventional numerical analysis includes three main steps:
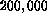states depending on the structure of the
CTMC and the available memory. Different algorithms for the calculation of the
steady state distribution are offered.
The idea of the structured analysis is to avoid the generation and storage of the complete generator matrix and instead exploit the model structure also for analysis. The underlying ideas are described in [9][7]. Here we give only a brief summary of the approach. In a first step the HQPN is transformed into a two level hierarchy including one HLQPN and several LLQPNs. Afterwards a single state in the complete state space can be represented by a unique state of the HLQPN and a unique state for every LLQPN. Therefore the complete state space can be generated by combining subspaces of the LLQPN state spaces according to a state of the HLQPN. Subspaces of LLQPN state spaces are defined by the marking of the places input and actual_population. Like the state space, the generator matrix is structured into submatrices according to the state of the HLQPN and every submatrix can be represented by the generalised tensor (kronecker) product/sum of submatrices describing local transitions in the LLQPNs. These structured representations of state space and generator matrix are very compact since the size of the overall state space and also the size of the generator matrix grows with the product of the sizes of LLQPN state spaces and matrices. Thus, the combination of a few LLQPNs, with a few hundred states each, yields an overall state space with several millions of states.
Structured analysis results from the observation that the matrix structure can be exploited during the analysis. Exploitation of this structure means that state space generation and iterative solution becomes more efficient in terms of memory requirements and sometimes also in terms of CPU time requirements. The underlying numerical techniques are essentially the same as in the conventional case, only the basic operation, the vector matrix multiplication, is implemented in a different form. Thus, structured analysis is an exact approach, as far as iterative numerical analysis techniques are exact, and does only rely on the hierarchical structure, not on symmetry assumptions. For structured analysis we have to perform the same three steps as above, however, the single steps are slightly different. Exploration of the state space consists of
This approach accelerates generation of the state space for large models, since a number of small state spaces instead of one very large state space is generated. Additionally the generation can be easily parallelised since state space and matrix generation for a LLQPN depend only on the state space of the HLQPN and not on other LLQPNs.
Subsequently the second step is performed and the Markov chain is analysed by an iterative technique using only HLQPN and LLQPN matrices. For details about the realisation of the algorithms we refer to [9][7]. The approach allows to analyse Markov chains with several millions of states, see Sec. 4 for an example. The last step is the computation of the required performance measures from the stationary solution vector, exactly as for a flat analysis.
An approximate analysis technique, which is integrated in QPN-Tool, is based on repeated aggregation/disaggregation of LLQPNs. State space generation for this method is performed as described above. However, for an analysis the complete probability distribution vector is never generated. Instead, the LLQPNs and the HLQPN are analysed in isolation by assuming all other parts of the model are aggregated. Analysis of an isolated LLQPN/HLQPN yields new parameters for the aggregates, which are used for the isolated analysis of other parts. This process is iterated until a fixed point is reached. Although the technique is a heuristic it often yields sufficiently accurate results in a very short time, even for large models.
The implemented structured analysis module currently supports two levels of the hierarchy, hierarchical LLQPNs are simply flattened and subsequently analysed. The approach can be extended to use several hierarchical levels, but this presumably does not extend the size of solvable models, since most of the memory is used for the vector rather than for the generator matrix representation. Thus, from a solution point of view it is not necessary to support more than two levels, however, for specification convenience arbitrary hierarchies are highly recommended and are supported in QPN-Tool.