![]() System analysis is often done with respect to qualitative and
quantitative aspects. E.g. one feature of a fault-tolerant computer is
that it will eventually recover from an error which is a qualitative
property of the system. A designer of such a system is surely also
interested in the time needed for recovery, a quantitative
property.
System analysis is often done with respect to qualitative and
quantitative aspects. E.g. one feature of a fault-tolerant computer is
that it will eventually recover from an error which is a qualitative
property of the system. A designer of such a system is surely also
interested in the time needed for recovery, a quantitative
property.
Several formalisms have been developed for modelling and analysing qualitative properties. Petri nets (PNs) [22][17] belong to these formalism. They have been proved to be suitable for representation of concurrency and synchronisation aspects in modern distributed systems. Since PNs do not involve any notion of time, temporal descriptions have been incorporated to render them suitable also for quantitative analysis leading to Timed and Stochastic Petri nets. A well-known representative of this class are Generalized Stochastic Petri nets (GSPNs) [2][1], which have been used for modelling a variety of systems [21][20][19][18].
Apart from concurrency and synchronisation another characteristic of distributed systems is sharing of common resources. Modelling this aspect, especially the scheduling rule, of a system using (GS)PN elements is quite difficult and leads to large and complex models [3].
Consider, e.g., a queue where  colours of tokens arrive according
to exponentially distributed interarrival times and whose service times
are exponentially distributed. If the scheduling strategy is FCFS, one
has to encode the colour of the token in each position of the queue.
Assume that an upper bound for the number of tokens in the queue is
given, e.g.
colours of tokens arrive according
to exponentially distributed interarrival times and whose service times
are exponentially distributed. If the scheduling strategy is FCFS, one
has to encode the colour of the token in each position of the queue.
Assume that an upper bound for the number of tokens in the queue is
given, e.g. 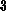 , then the GSPN in Fig. 1 would model the
queue accurately. Transitions
, then the GSPN in Fig. 1 would model the
queue accurately. Transitions 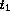 and
and 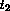 model the arrival of a
token of either colour and transitions
model the arrival of a
token of either colour and transitions 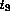 and
and 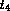 model the
service of the token in front of the queue. The places
model the
service of the token in front of the queue. The places 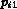 and
and
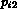 represent position
represent position 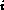 of the queue and the place
of the queue and the place 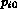 ensures that this position is occupied by at most one token. Since
entering a position is modelled by immediate transitions, a token
entering position
ensures that this position is occupied by at most one token. Since
entering a position is modelled by immediate transitions, a token
entering position 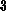 of the queue will immediately advance to
position
of the queue will immediately advance to
position  and
and 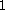 , if they are free. This way of modelling a FCFS
queue with GSPN elements works fine if an upper bound for the number
of tokens is known a priori. Performing several experiments with
different initial markings will necessitate a modification of the GSPN
model of the queue for each experiment. If there is no upper bound
known beforehand it is even more difficult. Other service times and
scheduling strategies lead to very complex models. If the service
time of a queue is specified by, e.g. a Coxian distribution and the
scheduling strategy is Last Come First Served - Preemptive Resume, it
becomes just about impossible to model such a queue with a GSPN.
, if they are free. This way of modelling a FCFS
queue with GSPN elements works fine if an upper bound for the number
of tokens is known a priori. Performing several experiments with
different initial markings will necessitate a modification of the GSPN
model of the queue for each experiment. If there is no upper bound
known beforehand it is even more difficult. Other service times and
scheduling strategies lead to very complex models. If the service
time of a queue is specified by, e.g. a Coxian distribution and the
scheduling strategy is Last Come First Served - Preemptive Resume, it
becomes just about impossible to model such a queue with a GSPN.
A popular modelling world to represent resource sharing are queues [15][7], where system behaviour can be modelled in a compact way. Receiving the benefits of both modelling worlds GSPNs have been enhanced by the usual descriptions of queues leading to a new model, Queueing Petri nets (QPNs) [3]. Queues can be directly integrated into Coloured GSPNs (CGSPNs) by associating them with the places of the net, since a basic property of queues is that customers entering the queue will eventually leave it. QPNs offer a specification paradigm where concurrency and synchronisation aspects are described by (CGS)PN elements and resource sharing is modelled by queues giving a structured model of a system.
Since analysis of modern systems can not be done without proper tool support, we have developed a program package (QPN-Tool) offering a convenient graphical user interface and several analysis algorithms for QPN models. Instead of specifying the transitions of a Coloured GSPN by predicates or functions, QPN-Tool automatically provides a local unfolding so that also unexperienced users can specify their QPN models. Furthermore QPN-Tool offers a variety of PN algorithms and automatically determines quantitative properties of the system employing efficient algorithms from PN and Markov theory. In Sect. 2 we introduce QPNs and the QPN-Tool is described in Sect. 3. A short comparison with other tools is given in Sect. 4.