Kanban System with Unreliable Machines
The model describes a production line with Kanban control, where machines
in the different productions cells may fail and need repair. It is assuemd
that idle machines cannot fail and that machines are repaired by a single
repairman who visits all cells in cyclic order. If a machine needs repair,
then the repairman first repairs the machine before travelling to the next
cell. The model is a performability model since it includes the description
of the performance due to the processing of parts and of the availability
due to failures and repairs of mschines. All times, namely arrival times
of parts, processing times, transfer times, time to failure of machines, reapir
times and travelling times are exponentially distributed. Thus, the net describes
a Markov chain. As usual for performability models, processing and transfer
of parts is much faster than failures and repairs of the machines, such that
the resulting Markov chain is stiff. If we structure the generator matrix
of the Markov chain according to th enumber of failed machines, than the
matrix prosesses NCD-property.
APNN-Description
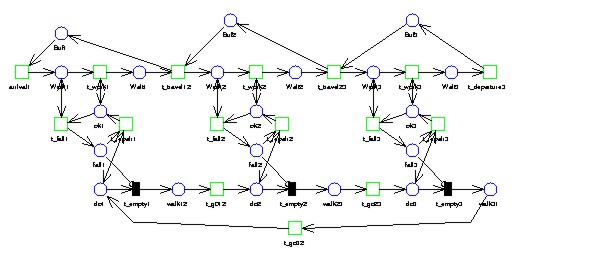
The model is described as a net. However, the places of the net are partioned
into disjoint subsets collecting all places belonging to one cell into one
subset. Places belonging to the repairman are collected in the last subset.
Automata-Description
The automata description of the example includes the matrices for a model
8 Kanban tickets and a single machine per cell which results in a CTMC
with 2,302,911 reachable states and 19,131,876 transitions.
- Matrices of the flat automata
network with a potential state space including 19,131,876 states.
- Matrices of the hierarchical
automata network with 40 states in the upper level and a potential
state space that is identical to the reachable state space.
References
- P. Buchholz, T. Dayar. Block SOR for Kronecker structured matrices.
Linear Algebra and Its Applications (to appear).
