Liveness

Liveness concerns the firing of transitions. Since transitions model activities, it is often desirable that no marking can be reached, such that a transition is never enabled again. If such situations are excluded the Place-Transition net is called live.

Definition (bounded, live, home state) Let 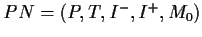$ PN = (P, T, I^-, I^+, M_0)$ be a Place-Transition net.

  1. PN is a bounded Place-Transition net, iff $ \forall p \in P:\exists k \in {\rm I\kern-0.25em N}_0:\forall M \in R(PN):M(p) \leq k$.
    PN is safe, iff $ \forall p \in P:\forall M \in R(PN):M(p) \leq 1$.
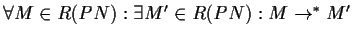  2. A transition $ t \in T$ is live, iff $ \forall M \in R(PN):\exists M\rq{} \in R(PN): M \rightarrow^{\ast} M\rq{}$ and $ M\rq{}[t>$.
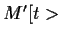    PN is live, iff all transitions are live, i.e. 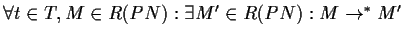$ \forall t \in T, M \in R(PN):\exists M\rq{} \in R(PN):M \rightarrow^{\ast} M\rq{}$ and $ M\rq{}[t>$.
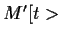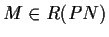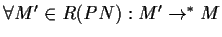  3. A marking $ M \in R(PN)$ is a home state, iff $ \forall M\rq{} \in R(PN):M\rq{} \rightarrow^{\ast} M$.


Lehrstuhl Informatik IV, Universität Dortmund
© 28.09.2001