Model checking
Model checking is a verification technique to determine if a system possesses a desired
property. In our context a system is specified as a Petri net and a property is
expressed as a temporal tree logic (CTL) or a linear temporal logic (LTL) formula.
The model checking problem for a given PN and a formula f is to decide
whether
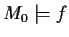 or not.
or not.
Computational Tree Logic
CTL is a specification language for a propositional, branching-time temporal
logic. The underlying set of atomic propositions consists of expressions considering
markings, e.g.
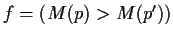 is such an atomic proposition for
is such an atomic proposition for
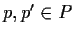 of PN. Every atomic proposition is a CTL formula; if
of PN. Every atomic proposition is a CTL formula; if 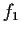 and
and
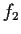 are CTL formulas, then so are
are CTL formulas, then so are
- (a)
-
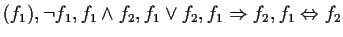 (with their usual meanings)
(with their usual meanings)
- (b)
-
![$ AF f_1, EF f_1, AG f_1, EG f_1, AX f_1, EX f_1, A[f_1 U f_2], E[f_1 U f_2]$](CTL7.gif)
The temporal operators are nexttime (X), globally (G),
sometime (or finally) (F) and until (U). A is the all path
quantifier and E is the exists path quantifier.
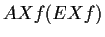 intuitively means, that
intuitively means, that 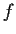 holds in every (in some) direct successor
holds in every (in some) direct successor
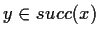 of marking
of marking 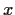 , resp.
, resp. 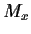 .
.
![$ A[f_1 U f_2]$](CTL13.gif) intuitively means, that every path has an initial prefix
intuitively means, that every path has an initial prefix 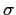 , such that
, such that 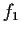 holds at all markings of
holds at all markings of 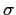 apart from the last one and
apart from the last one and 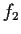 holds for the last marking of
holds for the last marking of
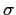 (
(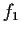 holds, until
holds, until 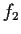 holds).
holds).
![$ E[f_1 U f_2]$](CTL15.gif) is analogously defined for some path.
is analogously defined for some path.
Common abbreviations of CTL formulas, their definition and intuitive meanings are as follows:
![$ AF f \equiv A[true U f]$](CTL16.gif) f is inevitable; finally f
f is inevitable; finally f
![$ EF f \equiv E[true U f]$](CTL17.gif) f potentially holds; f is possible
f potentially holds; f is possible
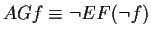 f is invariant; always f
f is invariant; always f
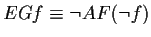 f potentially holds always
f potentially holds always
Links
Model-Checking Kit of TU München
Lehrstuhl Informatik IV, Universität Dortmund
© 28.09.2001