Petri nets

Petri nets were invented in 1962 by Carl Adam Petri and are a formalism for the description of concurrency and synchronistaion inherent in modern distributed systems. Since first described by Petri, many variations of his original nets have been defined such as Coloured Petri nets and a integation of time in Stochastic Petri nets.
Petri nets provide a convenient graphical representation of the system being modelled. The graphical representation of a Petri net comprises the following components:
places, drawn by circles. Places model conditions or objects, e.g., a program variable. Places might contain
tokens, drawn by black dots. Tokens represent the specific value of the condition or object, e.g., the value of a program variable.
transitions, drawn by rectangles. Transitions model activities which change the values of conditions and objects.
arcs, specifying the interconnection of places and transitions thus indicating which objects are changed by a certain activity.
Petri nets are bipartite graphs, i.e. we may only connect a place to a transition or vice versa, but we must not connect two places or transitions. This also would not make sense, if we keep the interpretation of place and transition in mind.

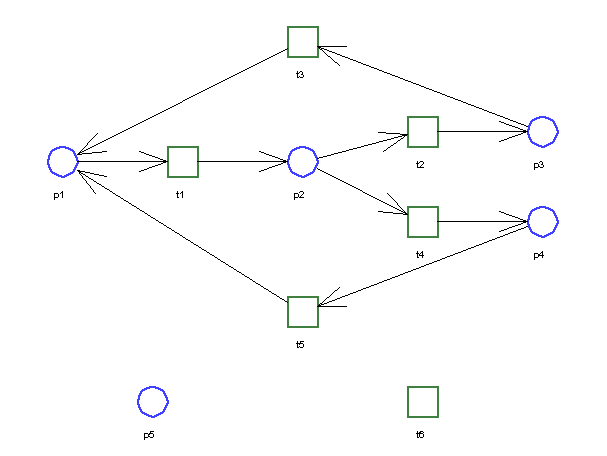In this figure place p1 is connected to transition t1. Because of the direction of the arc connecting p1 and t1 we will call p1 an input place of t1 and t1accordingly an output transition of p1. Places and transitions might have several input/output elements.
Place p5 and transition t6 are not interconnected to any other element. Such elements will be called isolated places or transitions. As expected, isolated elements of a Petri net do not influence the rest of the net and therefore we can neglect them.
Until now we have only described the static structure of a Petri net. Its dynamic behavior, can be expressed via the following rules:
Enabling of a transition:
A transition is enabled if all its input places are marked at least with one token.
Firing of an enabled transition:
An enabled transition may fire. If a transition fires, it destroys one token on each of its input places and creates one token on each of its output places.
Definition (Place-Transition net) A Place-Transition net is a 5-tuple

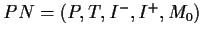where

$P = \{p_1,\ldots,p_n\}$ is a finite and non-empty set of places,
$T = \{t_1,\ldots,t_n\}$ is a finite and non-empty set of transitions,
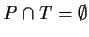$P \cap T = \emptyset$ ,
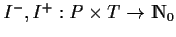$I^-,I^+:P \times T \rightarrow {\rm I\kern-0.25em N}_0$ are the backward and forward incidence functions, respectively
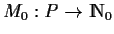$M_0:P \rightarrow {\rm I\kern-0.25em N}_0$ is the initial marking.

Coloured Petri nets

The tokens in Coloured Petri nets (CPNs) are attached by a type called the colour. CPNs were first defined by K. Jensen.

Definition (CPN) A Coloured Petri net (CPN) is a 6-tuple 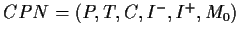, where

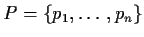$P = \{p_1,\ldots,p_n\}$ is a finite and non-empty set of places,
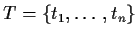$T = \{t_1,\ldots,t_n\}$ is a finite and non-empty set of transitions,
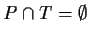$P \cap T = \emptyset$ ,
C is a colour function defined from 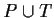$P \cup T$ into finite and non-empty sets,
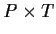are the backward and forward incidence functions defined on $P \times T$ such that
$I^-(p,t), I^+(p,t) \in [C(t) \rightarrow C(p)_{MS}], \forall (p,t) \in P \times T$ ,
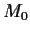is a function defined on P describing the initial marking such that
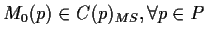$M_0(p) \in C(p)_{MS}, \forall p \in P$ .

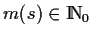Definition (Multi-set MS) A multiset m, over a non-empty set S, is a function $m \in [S \mapsto {\rm I\kern-0.25em N}_0]$ . The non-negative integer $m(s) \in {\rm I\kern-0.25em N}_0$ is the number of appearances of the element s in the multi-set m.

Stochastic Petri nets

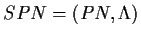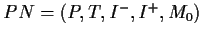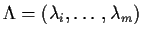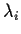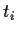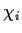The continuous-time Stochastic Petri net $SPN = (PN, \Lambda)$ is formed from the Place-Transition net by adding the set $\Lambda = (\lambda_i,\ldots,\lambda_m)$ to the definition. $\lambda_i$ is the, possibly marking dependent, transition rate of transition . I.e., the firing time is exponentially distributed and the distribution of the random variable $\chi_i$ of the firing time of transition 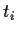is given by

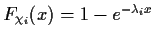$F_{\chi_i}(x)=1-e^{-\lambda_ix}$ .

Generalized Stochastic Petri nets

Generalized Stochastic Petri nets (GSPNs) have two different classes of transitions: immediate transitions and timed transitions. Once enabled, immediate transitions fire in zero time. Timed transitions fire after a random, exponentially distributed enabling time as in case of SPNs.

Definition (GSPN) A GSPN is a 4-tuple 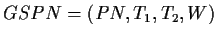where

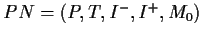is the underlying Place-Transition net,
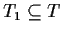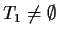$T_1 \subseteq T$ is the set of timed transitions, $T_1 \neq \emptyset$ ,
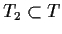$T_2 \subset T$ denotes the set of immediate transitions,
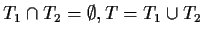
$T_1 \cap T_2 = \emptyset, T= T_1 \cup T_2$
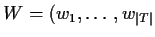is an array whose entry
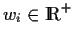
- is a (possibly marking dependent) rate of a negative exponential distribution specifying the firing delay, when transition 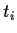is a timed transition, i.e. 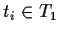$t_i \in T_1$ or
- is a (possibly marking dependent) firing weight, when transition 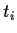is an immediate transition, i.e. $t_i \in T_2$ .