The QPN world

Queueing Petri Nets (QPNs) [6][4][3] combine Coloured Generalized Stochastic Petri Nets (CGSPNs) [10] with Queueing Networks (QNs) by hiding stations in special places of the CGSPN which are called timed places. The structure of a QPN is determined by a CGSPN with two types of places and transitions:

ordinary place

An ordinary place is equivalent to a place in a Coloured Petri net. Tokens fired onto such a place are immediately available for the corresponding output transitions.

timed place

A timed place contains a queue and a depository. A token which is fired on a timed place is inserted into the queue according to a scheduling strategy. The scheduling strategy determines which tokens in the queue are served. Each colour has an individual service time distribution of Coxian type. After receiving service the token moves to a depository, where it is available to the place's output transitions. 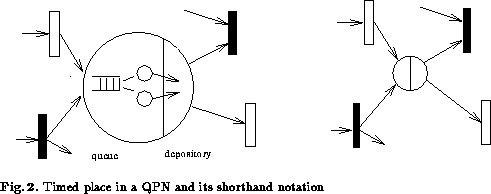Figure 2 presents a timed place and its graphical shorthand notation. A timed place can be regarded as a short notation of a complex CGSPN subnet, which models a Queueing Network service station. Scheduling strategies like FCFS, which concern the order of arrival, require a ranking of token colours to handle bulk arrivals. In case of a bulk arrival all tokens are separately inserted in succession into the queue in zero time. A token of the colour with the highest rank is inserted first.

immediate transition

An enabled immediate transition fires according to one of its colours without any delay in zero time. Any of its colours has a so called `firing frequency', which allows to compute firing probabilities in case of concurrently enabled immediate transitions.

timed transition

An enabled timed transition fires after a certain delay. This delay is determined by a colour-specific exponential distribution. Firing of timed transitions has a lower priority than firing of immediate transitions. Hence no timed transition can fire if an immediate transition is enabled. Like in GSPNs timed transitions obey a `race policy' to solve conflicts. Firing of a transition is always an atomic action.

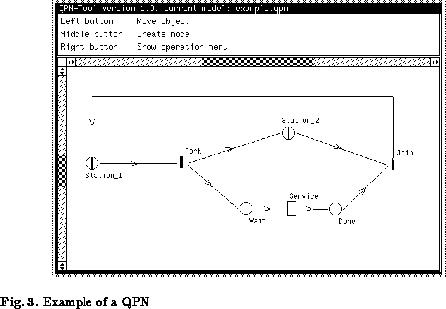
The following example focuses on the illustration of the different elements a QPN can contain and not on modelling anything of practical relevance.

Every QPN describes a stochastic process. A state of this process is determined by the cartesian product of the state descriptions at all timed places and the number of tokens at ordinary places with respect to their colours. If the service time within a timed place is modelled by an appropriate distribution, e.g. Cox-distribution, Markov-chain based analysis of the QPN is possible.

The state space is partitioned into two types of states similar to GSPNs (cf. [1]):

vanishing states

Firing of an immediate transition has a higher priority than any other change of state. Thus the stochastic process immediately leaves a state in which an immediate transition is enabled. If several immediate transitions are enabled, the one which fires first is determined by the firing probability. Firing probabilities are deduced from firing frequencies by relating a firing frequency to the sum of firing frequencies of all enabled transitions.

tangible states

If no immediate transition is enabled, firing of a timed transition or serving a token within a timed place can cause a change of state. The time for this change is determined by an exponential distribution in case of firing a timed transition or by the corresponding (exponential stage of the) service time distribution.