Queueing Networks (QNs) and Petri Nets (PNs) are well known formalisms for the description and analysis of a variety of systems. PNs are used for qualitative analysis whereas QNs are employed for performance evaluation (quantitative analysis). From a practical point of view, system analysis should be pursued with respect to both qualitative and quantitative aspects. Thus either one of the above formalisms is, in its pure form, incomplete. To overcome these insufficiencies, both formalisms have been enhanced in various ways by additional modeling features leading to new formalisms such as Timed and Stochastic Petri Nets [1] and Extended Queueing Networks [15].
In [16] Timed and Stochastic Petri Nets and Extended Queueing Networks are compared due to their expressive power and evaluation efficiency. One important result of the discussion there is, that certain specific deficiencies remain in both areas: Timed and Stochastic Petri Nets have, e.g., still difficulties in describing scheduling strategies in an appropriately compact manner; Extended Queueing Networks show, e.g., still deficits in describing sophisticated synchronization aspects.
Figure 1 illustrates this point for the well-known
Generalized Stochastic Petri Nets (GSPNs, [3][2]). The
GSPN models a queue serving two classes of tokens according to a
"preemptive-resume priority"- strategy, using standard PN elements. A
newly arriving token with higher priority (class 1) preempts the
service of the token being served at that moment. The preempted token
will continue its task, at the point of interruption, after completion
of service of all tokens with higher priority. Transition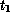 
is
enabled if preemption is to occur. Firing of 
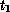preempts tokens
of class 2. The markings of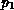 
and 
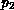keep track of the
occurrence of such a situation. This is the reason for modeling the
service of a token of class 1 by two identically parameterized timed
transitions. Note that this realization of a preemptive priority
scheduling strategy with resumption is only correct if exponentially
distributed service times are assumed; otherwise a yet more complex
model would have to be devised.
Describing such service time distributions and scheduling disciplines is straightforward in QNs. Only few efforts have been undertaken in the past to combine description features of QNs and PNs. In [4], e.g., QNs are exploited for determination of input parameters of a GSPN and vice versa, but there is no real combination of the two modeling formalisms on a description level. In [10] queues are integrated into timed transitions, which is unfavourable for retaining properties of the PN with regard to the timed net, since a token entering the queue might disable an already enabled transition. CPNs [11], like other High-level Petri Nets, provide data types of tokens for specifying queues. Incorporation of timing aspects into CPNs is under current research. Jensen [11] proposes to use a 'timed transition'-concept (cf. GSPNs) or to attach a time stamp to each token. Both suggestions have their difficulties in describing sophisticated scheduling disciplines or complex phase-type service time distributions. Furthermore the usual separation of load and machine aspects known from QN theory is not easy to establish in this context.
This article introduces a new version of the Queueing Petri Net (QPN) formalism [6][5] aiming at eliminating these difficulties. Apart from making description of complex systems easier, combining formalisms for the integrated specification of qualitative and quantitative aspects of a system also leads to new possibilities in analysis. This paper shows that particular qualitative properties of the QPN, being important preconditions for a quantitative analysis (especially Markovian analysis), can be obtained by exploiting efficient PN analysis techniques.
The article is organized as follows. In Sect. 2 some basic definitions are recalled. Section 3 gives a formal definition of queues. Queueing Petri Nets are introduced in Sect. 4. Section 5 explains the qualitative and quantitative analysis of QPNs and Sect. 6 is devoted to the application of efficient PN analysis algorithms for their qualitative analysis.