We will use the term 'Petri Nets' (PNs) for Place/Transition Nets [14] and its coloured version.
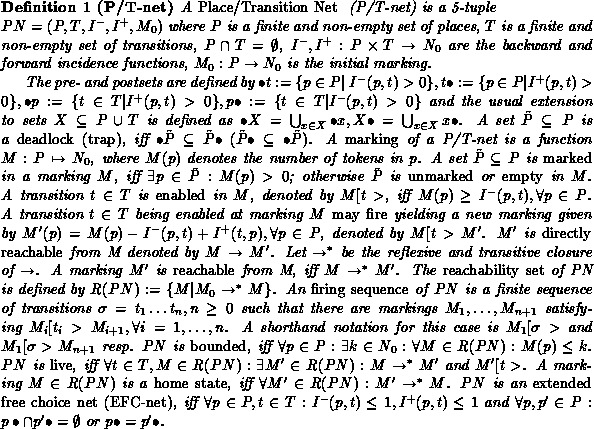
In order to better cope with graphical complexity, PNs with individual tokens have been introduced for the description of large and symmetric models. In this paper coloured PNs defined by K. Jensen are used and we limit the sets of colours to finite sets. For simplicity we will exploit the function representation of CPNs. The reader should note that the function representation corresponds to the expression representation of CPNs [11].
Every CPN can be unfolded into an uniquely determined Place/Transition Net. Thus all well known definitions and notions of Place/Transition Nets can be defined for CPNs via this transformation.
Qualitative analysis of (C)PNs consists of checking properties like boundedness and liveness. Efficient analysis techniques for (C)PNs include invariant analysis, reduction methods and the analysis of special net classes. Since a necessary condition for liveness in bounded nets is their strongly connectedness [9], we only consider such kind of nets in the following. Especially for a CPN we demand, that it is not the disjoint union of other CPNs.