A queue consists of a waiting area and a service center with one or more servers (cf. Fig. 2). A token arriving at a queue will immediately be served if a free server can be allocated to him or a token in service is preempted. Otherwise the arrived token has to wait in the waiting area until a server is dedicated to him. A queue-specific scheduling strategy determines the rules of serving tokens. Typical strategies are e.g. FCFS (first come first served) and PS (processor sharing). The service that a token demands is specified by the amount of time it would take the service center to perform this service. The usual notation for isolated queues is A/B/m-"scheduling strategy", where A denotes the probability distribution function (pdf) specifying the interarrival times of tokens, B is the pdf of service times and m is the number of servers.
In anticipation of the definition of QPNs, we will formally define a queue
to additionally contain a depository for served tokens.
These served tokens can be referred to as the tokens enabling transitions
of the QPN. A queue together with such a depository is called a 'timed
queueing place' in QPN terminology.
As indicated by the term 'timed queueing 
' there are also
'timeless queueing places', which are called 'immediate queueing places'
in analogy to the well-known GSPN terminology. Such queues are meant to model
only the scheduling aspect.
Figure 3 shows a (timed) queueing place and its pictorial shorthand notation.
Let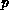 
denote such a queueing place and 
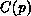the set of all colours
of tokens arriving at .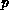 
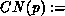
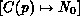is the set
of all functions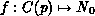 
. Such a function will specify the
'current marking' of the 'depository' (cf. Def. 2).
The pdf of service times is specified by the TR-function, if 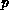is
a timed queueing place and the scheduling strategy is described by the
TR- and AC-functions. Here are some examples of timed queueing
places given by the usual Kendall notation and their corresponding
specification according to Def. 4.
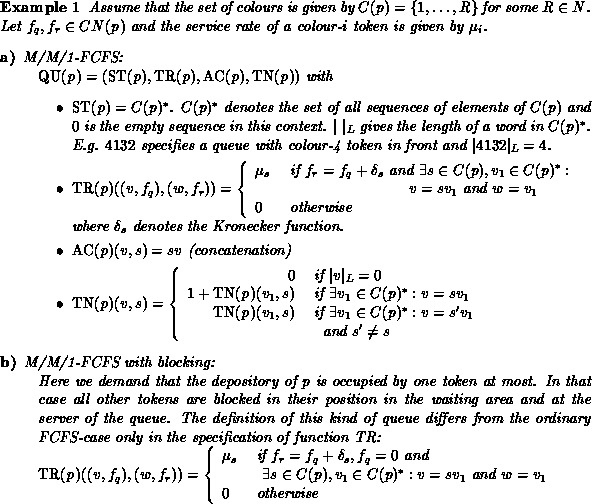
It is important to note that all these examples can also be viewed as descriptions of immediate queueing places. If the interarrival times are not known a priori, we will omit their description (e.g. -/M/1-FCFS), which does not affect the definition of queues.