Every QPN describes a stochastic process. Similar to the stochastic process specified by a GSPN [2], the states of this process might be vanishing or tangible. In vanishing states only immediate transitions are enabled and/or scheduling in immediate queueing places might occur. In tangible states a change to another state occurs due to the firing of a timed transition or some action concerning the service of a token in a queue of a timed queueing place.
For simplification of the formal description, we assume that timed queueing places
are numbered from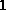 
to 
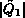and immediate queueing places
from 
to
.
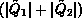Define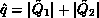 
and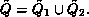 
Each state of a QPN is
an element of
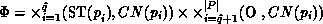The state space, denoted by 
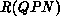, of the QPN's corresponding
stochastic process can be constructed like the reachability set of PNs.
We assume that the state space is finite. The initial state is given
by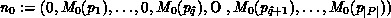 
where 
denotes the appropriate
element of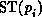 
.
In order to define the successor states of a given state we need the following definitions.
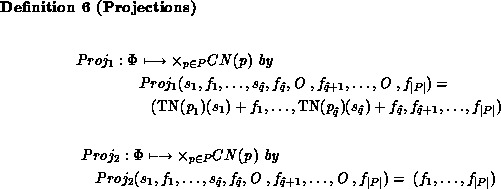
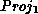maps a state of the QPN onto the corresponding marking of
the underlying CPN taking also tokens in queues into consideration.
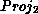neglects these tokens.
Furthermore in contrast to ordinary QNs we have to consider the case of bulk arrivals at the queue of a queueing place. There are several possibilities of defining the queue's state after acceptance of the new arriving tokens, e.g. apply the AC-function successively to randomly chosen elements of the bulk or define an order on arriving tokens. We choose the last possibility, assuming that the colours of all places are indexed by natural numbers and the smallest index specifies the colour with the highest rank. In case of bulk arrivals the AC-function can recursively be applied to the arriving tokens, which is described by a function R-AC defined as follows.
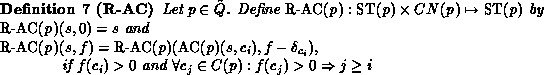
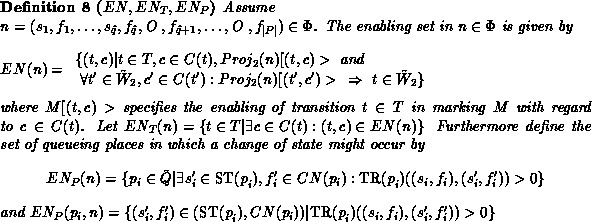
The definition of 
pays attention to the priority of immediate
transitions over timed transitions, thus if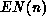 
is non-empty,
eithe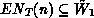r 
or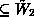 
holds.
The successor states of a given state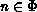 
can be calculated
as follows.
The relation between 
and one of its successor states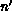 
will be denoted
by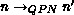 
and 
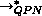is defined as the
reflexive and transitive closure of this relation.
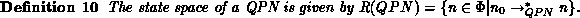
In the next subsections we will discuss qualitative and quantitative analysis of QPNs.