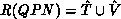 where
where
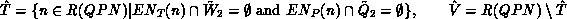 Let
Let 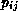 denote the probability of changing from
denote the probability of changing from 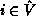 to
to 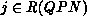 ,
,
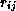 be the rate transiting from state
be the rate transiting from state 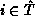 to
to
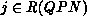 and
and 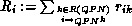 .
.
Quantitative analysis of QPNs can be performed by analysis of the embedded
Markov chain specified by the QPN's stochastic process. This procedure
is analogous to the quantitative analysis of GSPNs [2]. In the
following we assume that the QPN is bounded, implying a finite state space.
The state space of a QPN is the disjunct union of tangible and vanishing states,
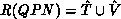 where
where
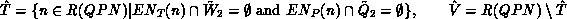 Let
Let 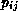 denote the probability of changing from
denote the probability of changing from 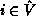 to
to 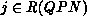 ,
,
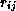 be the rate transiting from state
be the rate transiting from state 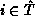 to
to
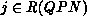 and
and 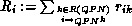 .
.
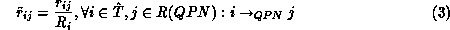
specifies the corresponding probability. Define four matrices
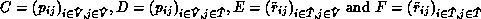 .
.
Since the sojourn time in vanishing states is zero by definition, we are only interested in tangible states. Thus it is sufficient to solve the global balance equations of the reduced embedded Markov chain given by
provided 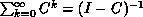 exists. If (4)
has a unique solution the steady state distribution of the QPN's stochastic
process is given by
exists. If (4)
has a unique solution the steady state distribution of the QPN's stochastic
process is given by
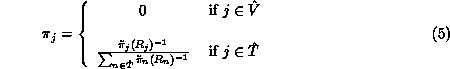
Performance measures can be computed from this steady state distribution as usual.
The description above shows that two important preconditions have to be satisfied for a successful quantitative analysis of QPNs:
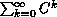 must exist and
must exist and
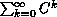 corresponds to the notion
'trap'.
corresponds to the notion
'trap'.
Define 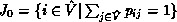 and
and
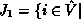
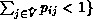 , i.e
, i.e
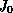 and
and 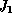 contain all vanishing states for which the sum of elements
of the corresponding row in matrix
contain all vanishing states for which the sum of elements
of the corresponding row in matrix  equals one or is smaller than one resp.
Note that, being in a vanishing state, a tangible state can only be reached via some
state of
equals one or is smaller than one resp.
Note that, being in a vanishing state, a tangible state can only be reached via some
state of 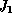 .
.
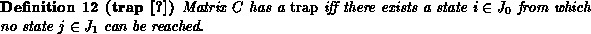
In QPN terminology this condition is specified by:
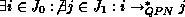 .
.
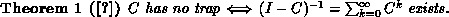
Matrix  characterizes the changes between vanishing states. Such states
are determined by enabling of immediate transitions or scheduling
in immediate queueing places according to the QPN
description. Thus, if matrix
characterizes the changes between vanishing states. Such states
are determined by enabling of immediate transitions or scheduling
in immediate queueing places according to the QPN
description. Thus, if matrix  contains a trap this indicates the
possible occurrence of an infinite firing of immediate transitions
or in pathological cases an infinite number of actions in an immediate
queueing place.
Therefore we will refer to this situation calling it a 'timeless trap'.
Figure 6 is meant to illustrate a timeless trap
caused by never ending firings of immediate transitions.
The next theorem proves that in a live QPN the stochastic process can not
be "caught" in such timeless traps.
contains a trap this indicates the
possible occurrence of an infinite firing of immediate transitions
or in pathological cases an infinite number of actions in an immediate
queueing place.
Therefore we will refer to this situation calling it a 'timeless trap'.
Figure 6 is meant to illustrate a timeless trap
caused by never ending firings of immediate transitions.
The next theorem proves that in a live QPN the stochastic process can not
be "caught" in such timeless traps.
implying that matrix  has no trap.
has no trap.
Proof:
Assume there is a trap, i.e.
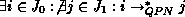 .
.
Consider the case 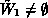 . Choose an arbitrary transition
. Choose an arbitrary transition
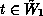 and a colour
and a colour 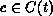 . Liveness yields
. Liveness yields
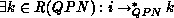 and
and 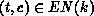 and
and 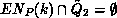 .
Thus
.
Thus 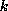 is a tangible state which can only be reached from
is a tangible state which can only be reached from  via some
state
via some
state 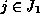 .
.
In the case of 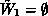 choose an arbitrary timed queueing place
choose an arbitrary timed queueing place
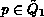 ,
, 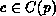 and a transition
and a transition 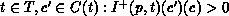 .
Liveness implies that there exists an infinite firing sequence containing
.
Liveness implies that there exists an infinite firing sequence containing
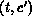 , thus colour
, thus colour  tokens are fired infinitely often onto place
tokens are fired infinitely often onto place 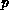 .
From (#>
.
From (#>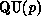 increases.
Because of our assumption all states reached from
increases.
Because of our assumption all states reached from 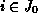 are vanishing, thus
the internal state
are vanishing, thus
the internal state 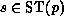 of
of 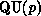 is only modified by the
AC-function, so that the token number of
is only modified by the
AC-function, so that the token number of 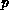 is not upper bounded,
contradicting the boundedness requirement.
Note, (#>
is not upper bounded,
contradicting the boundedness requirement.
Note, (#>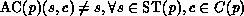 .
.



 =0
=0
So in bounded and live QPNs the existence of 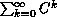 is guaranteed.
The second requirement, a unique solution of (4),
is satisfied if the state space of the reduced embedded Markov chain
contains only one irreducible subset of states, provided the state space
is finite. There is only one such subset iff
the QPN has at least one home state.
is guaranteed.
The second requirement, a unique solution of (4),
is satisfied if the state space of the reduced embedded Markov chain
contains only one irreducible subset of states, provided the state space
is finite. There is only one such subset iff
the QPN has at least one home state.
Summarizing all arguments we realize that quantitative analysis of QPNs can be performed by steady state analysis of the reduced embedded Markov chain, if the QPN is bounded, live and has home states. With that, qualitative properties of the QPN are essential preconditions for a successful quantitative analysis.
The next section is dedicated to a more efficient determination of some of these properties by exploiting the PN part of the QPN.