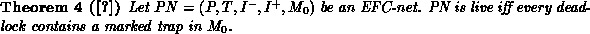
Liveness of the (C)PN need not carry over to the timed net [7][6][5]. Formulating restrictions on the incorporation of timing aspects for general QPNs is difficult, but we can establish such conditions, if we restrict the structure of the CPN to EFC-nets for which liveness can be determined very efficiently by examinating the deadlock/trap-property [12].
For liveness of an EFC-QPN, whose underlying CPN is live, obviously
immediate and timed transitions must not be in conflict. Furthermore
we have to ensure that all tokens in a queueing place have the
opportunity of being served independently of each other. Otherwise
also very simple QPNs need not be live. Fig. 7 depicts
such a situation. 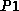 is a timed queueing place, whose queue service
tokens according to a 'last come first served preemptive resume'
scheduling discipline. Since firing of immediate transitions has
priority on scheduling in timed queueing places, a token being served
at
is a timed queueing place, whose queue service
tokens according to a 'last come first served preemptive resume'
scheduling discipline. Since firing of immediate transitions has
priority on scheduling in timed queueing places, a token being served
at 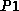 immediately returns to this place thus preempting service of
the other token. So either token
immediately returns to this place thus preempting service of
the other token. So either token  or
or 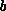 will never leave this
queue. The following conditions exclude such situations.
will never leave this
queue. The following conditions exclude such situations.
Part (10) of condition EQUAL-Service together with
(#>
Proof:
Assume there is a timeless trap, i.e. 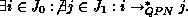 The set
The set
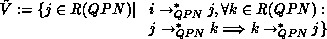 is a closed subset of states being reachable from
is a closed subset of states being reachable from 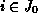 . Since
. Since
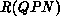 is finite,
is finite, 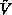 is non-empty.
is non-empty.
First of all we will show, that there is a state in 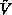 in which an immediate transition is enabled, i.e.
in which an immediate transition is enabled, i.e.
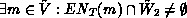 .
Assume the contrary.
From liveness of the CPN and (#>
.
Assume the contrary.
From liveness of the CPN and (#>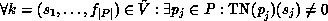 .
Choose an arbitrary state
.
Choose an arbitrary state 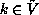 .
.
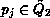 with
with
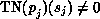 , an immediate transition is enabled, because
of our initial assumption that a timeless trap exists.
, an immediate transition is enabled, because
of our initial assumption that a timeless trap exists.
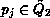 with
with
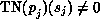 and since
and since 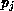 satisfies condition
EQUAL-Service the process will eventually reach a state
satisfies condition
EQUAL-Service the process will eventually reach a state 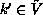 where
where 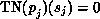 . This argumentation can be applied successively
to all
. This argumentation can be applied successively
to all 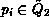 with
with 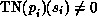 .
Thus a state
.
Thus a state 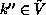 will be reached where
will be reached where
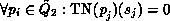 .
In analogy to (1st) the enabling of an immediate transition is
guaranteed.
.
In analogy to (1st) the enabling of an immediate transition is
guaranteed.
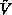 is a closed subset of states all these immediate
transitions are live with regard to
is a closed subset of states all these immediate
transitions are live with regard to 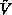 .
Let
.
Let
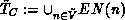 be the set of such live
immediate transitions with regard to colours
be the set of such live
immediate transitions with regard to colours 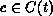 and
and
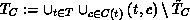 the corresponding complementary set.
the corresponding complementary set.
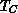 is non-empty, because of
is non-empty, because of 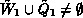 .
.
Boundedness and liveness of the CPN yield that the unfolded CPN consists
of P/T-nets which are by themselves strongly connected (cf. [9]).
Note that unfolding of a CPN might result in several isolated P/T-nets.
E.g. unfolding the CPN given in Fig. 7 yields two (strongly connected)
P/T-nets.
Define
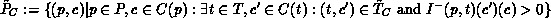 the set of input places of enabled transitions in
the set of input places of enabled transitions in 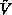 with
regard to the corresponding colours and
with
regard to the corresponding colours and
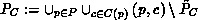 .
.
Due to strongly connectedness one of the following two cases must hold:
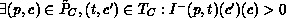
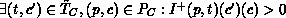
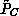 implies the existence
of
implies the existence
of 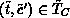 . Condition
EQUAL-Conflict together with the EFC-net structure ensures that
for
. Condition
EQUAL-Conflict together with the EFC-net structure ensures that
for 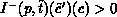 and
and
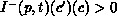 also transition
also transition 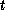 is enabled with regard to
is enabled with regard to
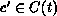 whenever
whenever 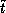 is enabled with regard to
is enabled with regard to
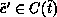 . Thus
. Thus 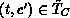 contradicting
contradicting 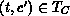 .
.
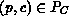 tokens of colour
tokens of colour
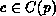 are not removed by firing of an immediate
transition
are not removed by firing of an immediate
transition 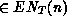 for some
for some 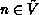 .
For
.
For 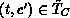 and
and 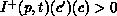 , tokens
of colour
, tokens
of colour 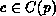 will pile up at place
will pile up at place 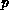 . Since
all queueing places keep track of the token count according to
(#>
. Since
all queueing places keep track of the token count according to
(#>


 =0
=0
Proof: For abbreviation some of the definitions given in the proof of Lemma 1 will be used here.
Assume the QPN is not live.
According to Theorem 3 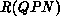 is finite.
Choose an arbitrary strongly connected subset
is finite.
Choose an arbitrary strongly connected subset
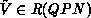 with
with 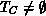 . This is always possible, since the
. This is always possible, since the 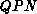 is assumed to be not live. Note that
is assumed to be not live. Note that 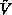 might also comprises
tangible states in this context.
might also comprises
tangible states in this context.
The EFC-net structure yields
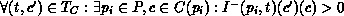 and
and 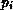 is not marked with any token of colour
is not marked with any token of colour 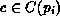 in all states
of
in all states
of 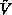 , i.e.
, i.e. 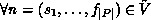 :
:
Otherwise, because conditions EQUAL-Service and EQUAL-Conflict are
satisfied, 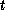 will eventually be enabled according to colour
will eventually be enabled according to colour 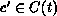 , since the QPN has no timeless trap (cf. Lemma 1).
Thus
, since the QPN has no timeless trap (cf. Lemma 1).
Thus
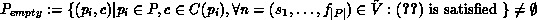 .
Extending the
.
Extending the  -operator to CPNs via unfolding
we get
-operator to CPNs via unfolding
we get 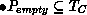 and
and 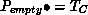 implying
implying 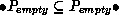 .
Since all queues keep track of the token number (cf. (#>
.
Since all queues keep track of the token number (cf. (#>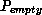 represents an unmarked deadlock of the CPN
contradicting its liveness (cf. Theorem 4).
represents an unmarked deadlock of the CPN
contradicting its liveness (cf. Theorem 4). 


 =0pt=0
=0pt=0