Markov Decision Processes (MDPs) are a commonly used model type to describe decision making in stochastic models. However, usually the parameters of MDPs result from some data or estimates of experts. In both cases parameters are uncertain. This uncertainty has to be taken into account during the computation of policies that describe decisions to be made over time. In this case, the parameters of the MDP are not exactly known, instead a set of MDPs is defined which captures the parameter uncertainty. The goal is then to find a policy that behaves good for all possible realizations of uncertainty. A good behavior is not really well-defined, common interpretations are an optimal policy for the worst possible realization of uncertainty (robust optimization), an optimal policy for the expected behavior (risk neutral stochastic optimization), an optimal policy for the expected behavior plus some guarantee for the worst case (stochastic optimization with some baseline guarantee), etc. In general, the computation of optimal policies for MDPs with uncertain parameters becomes much more complex than the computation of optimal policies for MDPs with known parameters. Many problems are NP-hard. However, often good approximation algorithms can be found to compute acceptable policies sometimes even with an error bound.

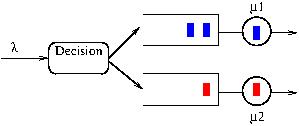
Queuing Network Example
MDPs with uncertain parameters appear in in various application areas like the control of queuing networks, maintenance problems, routing in computer networks, computer security or computational finance. In the figure above a small control problem for queuing networks is shown. Upon arrival of a new task it has to be decided into which queue the entity is routed. The routing algorithm knows the number of customers in each queue but not the detailed service times. In an MDP setting the rates are known, internal uncertainty is introduced by different realizations of the (exponentially distributed) service and inter arrival times. With uncertain parameters the rates are not exactly known introducing another source of external uncertainty
The basic assumption of rectangular parameter uncertainty is that uncertainty occurs independently for every state-action pair (s,a). A typical example are Bounded Parameter MDPs (BMDPs) where transition probabilities or/and rewards are defined by intervals rather than scalars. For rectangular uncertainty, the robust policy, which maximizes the reward under the worst possible realization of uncertainty, can be computed with polynomial effort. However, the computational effort is still much higher than the effort required to compute optimal policies for MDP with known parameters. In particular, solution approaches based on linear programming cannot be applied for the analysis of BMDPs or related models.
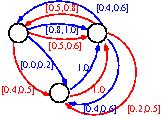
BMDP Example
In our research on MDPs with rectangular uncertainty, mainly BMDPs
have been analyzed. The specification of BMDPs with a class of
Stochastic Petri Nets has been published in [1], [6] describes the
application of BMDPs for maintenance problems. In [4] numerical
methods to compute robust policies for BMDPs are compared and [3]
describes the relation between aggregation of large MDPs and the use
of BMDPs.
Approximate and exact methods for two NP-hard problems
are considered in the papers [2] and [7]. In [2] the Pareto frontier
of policies that are not dominated with respect to their worst,
average and best case behavior is approximated. [7] introduces
several algorithms to determine policies that are optimal according
to one criterion, like the average or worst case, and guarantee a
minimal reward for the other criterion.
In the scenario based approach, uncertainty is represented by finitely many scenarios. This allows one to consider correlations between different parameters of the model or to sample from a set of parameter distributions. The goal is then to find a policy which maximizes the weighted sum of rewards over all scenarios. The resulting optimization problem has shown to be NP-hard [1].
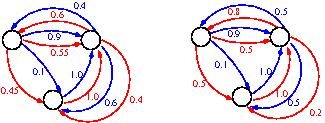
Example of a Concurrent MDPs with two Scenarios
The class of Concurrent MDPs (CMDPs) has been defined in [2,8]. Paper [8] also presents several methods to compute or approximate optimal policies. The approach is extended to a new class of policies and decision dependent rewards in [9].
Marco Beccuti, Elvio Gilberto Amparore, Susanna Donatelli, Dimitri Scheftelowitsch, Peter Buchholz, Giuliana Franceschinis: Markov Decision Petri Nets with Uncertainty. EPEW 2015: 177-192
Dimitri Scheftelowitsch, Peter Buchholz, Vahid Hashemi, Holger Hermanns: Multi-Objective Approaches to Markov Decision Processes with Uncertain Transition Parameters. VALUETOOLS 2017: 44-51
Peter Buchholz, Iryna Dohndorf, Alexander Frank, Dimitri Scheftelowitsch: Bounded Aggregation for Continuous Time Markov Decision Processes. EPEW 2017: 19-32
Peter Buchholz, Iryna Dohndorf, Dimitri Scheftelowitsch: Analysis of Markov Decision Processes Under Parameter Uncertainty. EPEW 2017: 3-18
Dimitri Scheftelowitsch: Markov decision processes with uncertain parameters. Dissertation Technical University of Dortmund, Germany, 2018
Peter Buchholz, Iryna Dohndorf, Dimitri Scheftelowitsch: Time-Based Maintenance Models Under Uncertainty. MMB 2018: 3-18
Peter Buchholz, Dimitri Scheftelowitsch: Light robustness in the optimization of Markov decision processes with uncertain parameters. Computers & OR 108: 69-81 (2019)
Peter Buchholz, Dimitri Scheftelowitsch: Computation of weighted sums of rewards for concurrent MDPs. Math. Meth. of OR 89(1): 1-42 (2019)
Peter Buchholz, Dimitri Scheftelowitsch: Concurrent MDPs with Finite Markovian Policies. Accepted for MMB 2020
A collection of Matlab functions which implements the algorithms from [8] and [9] can be downloaded (please cite the above references if you use the software).